Problema 3 cuerpo Se trata de una nueva serie de ciencia ficción de Netflix, una de las más esperadas del año, y está basada en la novela homónima del escritor chino Liu Cixin. El título hace referencia a uno de los temas más conocidos y discutidos de la mecánica celeste, la disciplina que estudia el movimiento de planetas, satélites, asteroides y otros cuerpos utilizando un enfoque de física matemática. El verdadero «problema de los tres cuerpos» es central en la historia del libro y también tiene un cierto significado en la serie de televisión, que, sin embargo, se tomó algunas licencias al distanciarse parcialmente de los acontecimientos imaginados por Liu Cixin.
De aquí en adelante es necesario un pequeño spoiler para contextualizar la explicación que sigue, ya que revela cosas que no se pueden deducir del título del libro o de la serie en sí: aquellos que realmente no quieren saber nada. Al respecto puede saltarse los dos párrafos siguientes.
En la novela
El libro se mueve entre el pasado, el presente y el futuro, y narra el contacto de la humanidad con una civilización extraterrestre que vive en un sistema solar diferente al nuestro. Uno de los protagonistas de la historia descubre lo que parece ser un videojuego en el que hay que intentar sobrevivir en una civilización que habita en un determinado planeta, donde se suceden “eras del orden” mientras el día y la noche se alternan y el día y la noche se alternan. . Las estaciones son regulares y los períodos son «edades del caos», donde las estaciones y los días son períodos diferentes y muy irregulares. En «Ages of Order» la civilización florece y se desarrolla, mientras que en «Ages of Chaos» es aniquilada debido a las condiciones inhabitables en las que termina el planeta.
Las simulaciones de videojuegos continúan a lo largo de gran parte del libro, mientras que mientras tanto suceden otras cosas en diferentes niveles narrativos y épocas que nos ayudan a comprender de qué se trata realmente este juego. Por tanto, queda claro que la dificultad radica en el hecho de que el mundo del videojuego está ubicado en un sistema de tres estrellas, que interactúan gravitacionalmente entre sí y de esta manera también afectan la órbita del planeta, que alterna fases más estables. con caóticos, con inviernos muy largos y fríos, días con momentos de luz que duran unos instantes o duran mucho tiempo, marcan el final (o más bien la suspensión) de gran parte de la vida.
El problema de los tres cuerpos
El problema de los tres cuerpos en particular es que es difícil predecir con precisión la forma en que se mueven los tres cuerpos celestes y la evolución del sistema que forman. Es una cuestión que ha fascinado a matemáticos, astrónomos y astrofísicos durante siglos y que, contrariamente a la creencia popular, no siempre es irresoluble. Profundizándolo, a lo largo de los años ha sido posible comprender mejor cómo funcionan las órbitas de los cuerpos celestes y, sobre todo, entender cómo explotarlas, por ejemplo, gestionando misiones espaciales interplanetarias utilizando sondas creadas para explorar nuestro sistema solar.
Como aprendimos en la escuela, el Sol es, con diferencia, el cuerpo más grande de nuestro sistema solar y, debido a su capacidad para atraer otros cuerpos (Interacción de gravedadEn el sentido de la física clásica, o simplemente lo que llamamos «fuerza gravitacional») depende en gran medida de la masa, el Sol pudo retener los planetas (en términos cósmicos) y hacerlos girar alrededor de sí mismo. Los planetas también producen interacciones gravitacionales entre sí, pero todas estas interacciones son insignificantes porque su masa es incomparable con la masa del Sol (la masa de este último, por ejemplo, es más de 330.000 veces la de la Tierra).
A finales del siglo XVII apareció el matemático y físico inglés Isaac Newton. Formalizar Ecuaciones de movimiento y gravedad de los cuerpos celestes, de modo que podemos calcular en principio dónde estará el cuerpo que orbita a otro en un momento dado conociendo la posición inicial, la velocidad y algunas otras variables. Las leyes del movimiento de Newton se basaron en trabajos y estudios previos realizados por otros científicos importantes, como el astrónomo alemán Kepler, quien formuló las leyes que rigen los movimientos de los planetas.
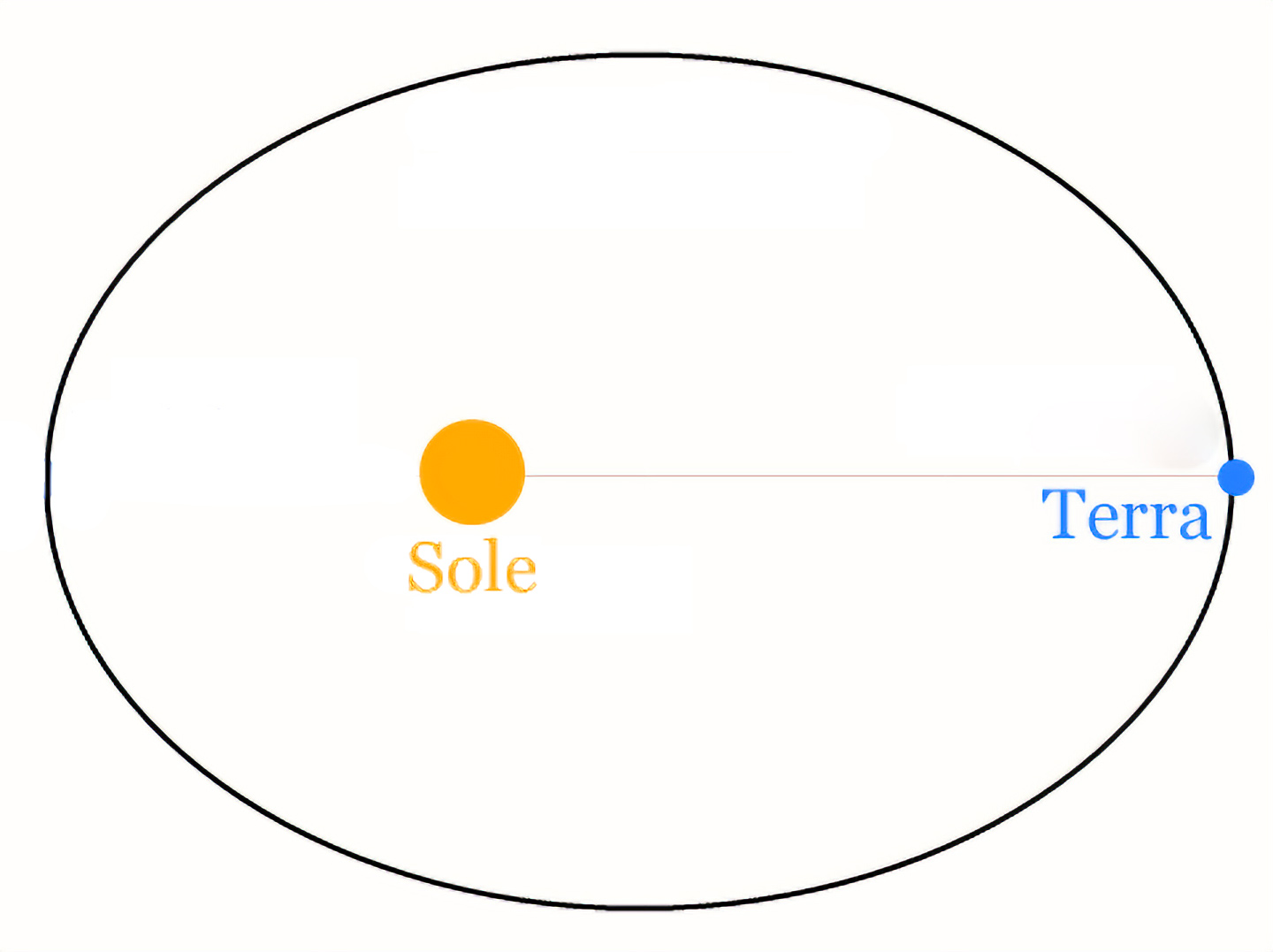
Utilizando las leyes y ecuaciones de Newton, se pueden calcular con precisión las órbitas prescritas de dos cuerpos unidos por interacción gravitacional. Las formas de estas órbitas pueden ser un círculo, una elipse, una parábola o cualquier otra sección cónica (formas que se pueden obtener cortando un cono). La Tierra, por ejemplo, describe una órbita elíptica alrededor del Sol.
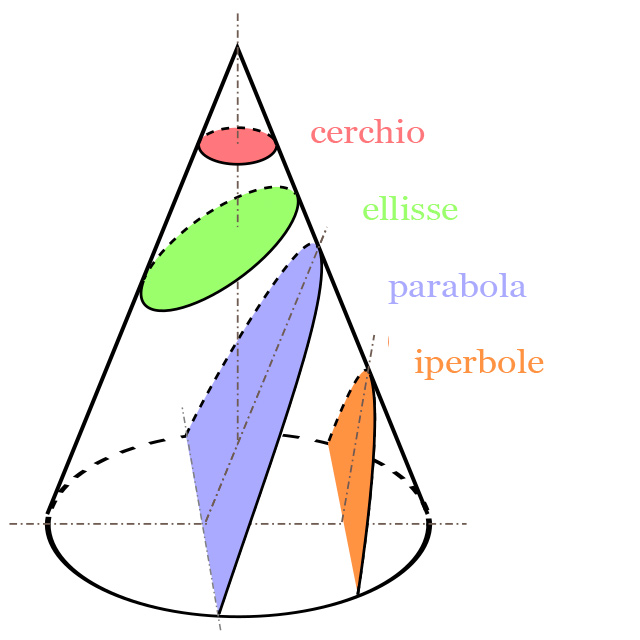
(Wikimedia)
Las leyes de Newton brindan soluciones simples cuando se considera un escenario en el que sólo hay dos cuerpos celestes interactuando entre sí en todo el universo: el «sistema de dos cuerpos». Una vez que intentas agregar un tercer objeto, las cosas se complican mucho ya que las órbitas se vuelven irregulares y, a menudo, impredecibles a largo plazo. En este caso, conocer la posición inicial y la velocidad de los objetos ya no es suficiente para hacer predicciones precisas porque todo se vuelve caótico, y siempre después de un cierto período de tiempo uno de los tres objetos es expulsado del sistema.
Sinceramente, cualquier sistema con más de dos cuerpos es un problema y por eso generalmente hablamos de «problema corporal sustantivo, masculino—«, donde «n» representa cualquier número. Es una cuestión que ha fascinado y ocupado a muchos matemáticos, físicos y astrónomos desde la época de Newton, cuando la gente empezó a preguntarse cómo predecir las órbitas de los cuerpos celestes en sistemas más complejos. Y no era sólo una cuestión teórica: predecir los movimientos de la Luna y los planetas era esencial para la navegación marítima, por ejemplo, y más recientemente se ha vuelto esencial para organizar misiones espaciales.
Pronto quedó claro que el problema de los n cuerpos, al menos para nuestros vecinos cósmicos, no era insoluble, siempre que estuviéramos satisfechos con algún grado de aproximación. De hecho, un sistema que contiene múltiples cuerpos celestes suficientemente distantes entre sí puede visualizarse como una serie de sistemas de dos cuerpos. En el caso del sistema solar, este trabajo se ve facilitado por la presencia de una estrella, el Sol, que, como hemos visto, tiene una fuerte influencia sobre todo lo demás debido a su enorme masa. Así, podemos pensar a grandes rasgos en sistemas de dos cuerpos que siempre incluyen al Sol y uno de los otros planetas, descuidando todo lo demás.
De esta forma obtenemos un sistema solar en el que cada planeta completa una órbita elíptica alrededor del Sol como predicen las leyes de Kepler. Es una aproximación más que aceptable al horizonte temporal de nuestra existencia y al de toda la especie humana, considerando que cualquier cambio en las órbitas debido a interacciones gravitacionales mínimas se hace perceptible a lo largo de millones, si no miles de millones de años.
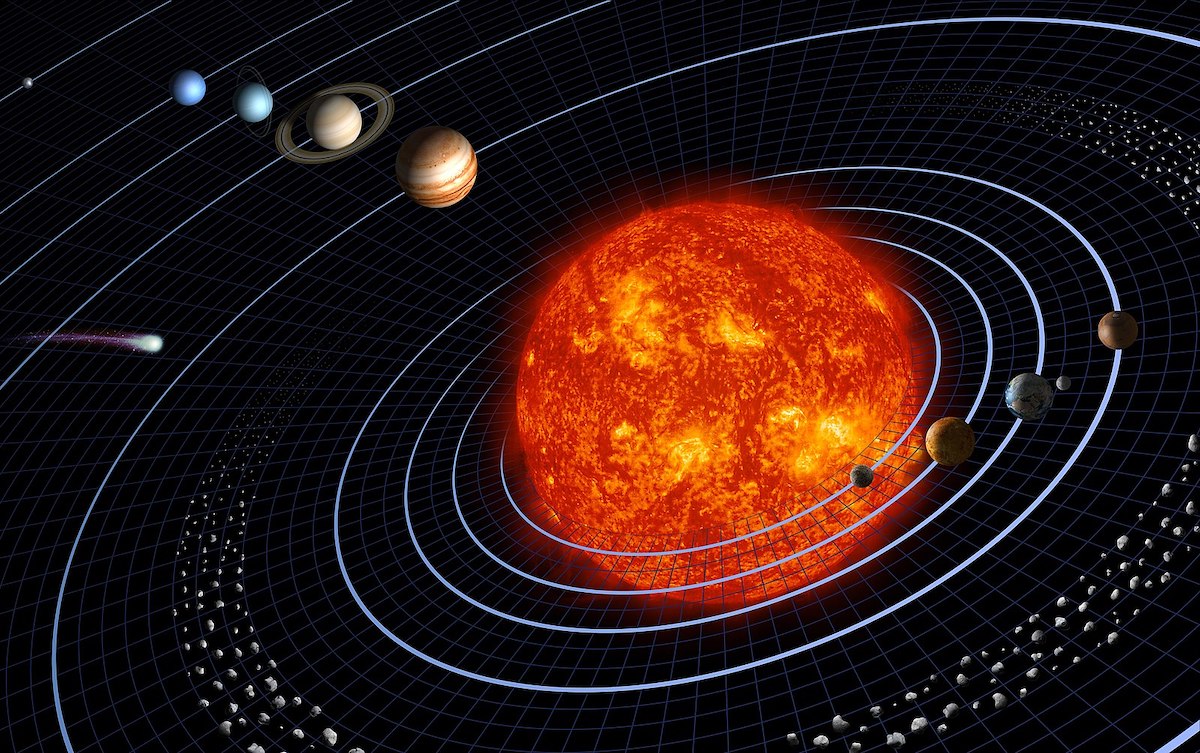
Representación a escala del sistema solar (NASA)
Estas soluciones menos que ideales caen en lo que se llama «Problema de tres objetos encuadernados«, donde es aceptable obtener la mejor aproximación posible al movimiento de los cuerpos celestes. En el caso del sistema solar, esto se hace asumiendo, por ejemplo, que tienen una masa insignificante en comparación con el Sol y también con respecto a Júpiter, que es el planeta más grande de la familia de ocho planetas, incluida esa tierra claramente.
Para quienes estudian sus órbitas, nuestro sistema solar también ofrece la ventaja de tener una sola estrella, a diferencia de muchos otros sistemas que tienen dos estrellas (“sistemas binarios”). Los soles de estos últimos suelen formar órbitas estables alrededor de un punto determinado que corresponde a su centro de masa. Los planetas de los sistemas binarios suelen tener órbitas estables debido a su distancia y menor masa en comparación con las estrellas, por lo que sus movimientos a lo largo del tiempo pueden predecirse con una buena aproximación.
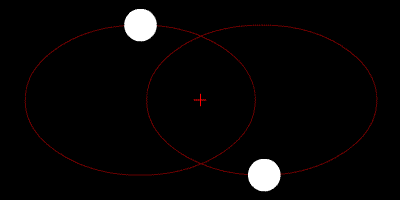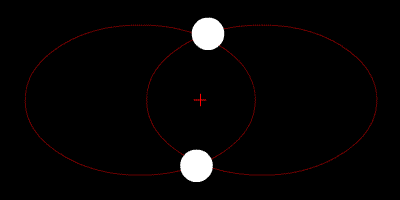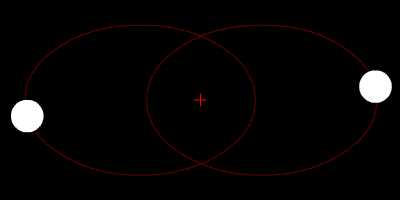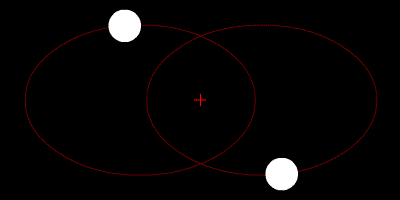
Sin embargo, hay formas de trabajar en el problema de los tres cuerpos y obtener resultados lo más cercanos posible a la realidad. Sólo una porción muy pequeña de la ruta se puede calcular con precisión, por lo que si divide todo el problema en pequeñas secciones, puede calcular los movimientos de todos los objetos en el sistema en un corto período de tiempo y actualizarlos a medida que calcula las secciones. (Matemáticamente hablando, se dice que la integración numérica se realiza para resolver ecuaciones diferenciales).
Aplicando esta técnica obtenemos una simulación de n cuerpos, es decir, una simulación para predecir los movimientos de un determinado número de planetas incluso en un futuro muy lejano. Se pueden utilizar simulaciones para intentar predecir la formación o evolución de galaxias enteras, es decir, una gran colección de sistemas solares, estrellas, polvo y gas interestelar. Hoy en día estos cálculos se hacen mediante ordenadores muy potentes, mientras que antes había que hacerlos manualmente con mucha paciencia y riesgo de cometer más errores.
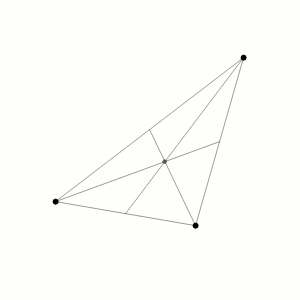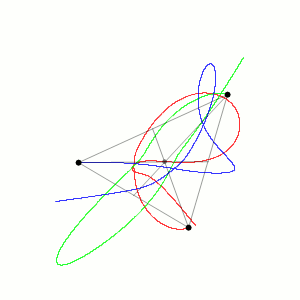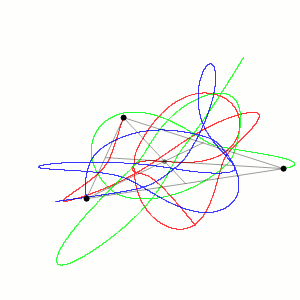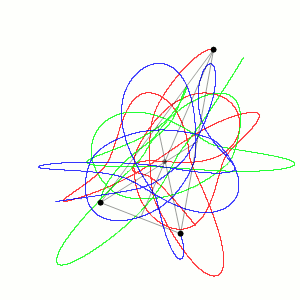
Aproximación de las trayectorias de tres cuerpos idénticos cuyo centro de masa permanece constante (Wikimedia)
Muchos matemáticos y astrónomos han abordado el problema de los tres cuerpos para encontrar casos específicos en los que se pueda encontrar una solución funcional completa sin aproximaciones (es decir, una solución analítica). En el siglo XVIII, el matemático suizo Euler encontró A Una serie de soluciones Tres hipotéticos cuerpos celestes siempre permanecen alineados a lo largo de una línea recta imaginaria que pasa por su centro de masa. El italiano Joseph Louis Lagrange encontró una solución más elegante al problema de los tres cuerpos, cuenta Puntos en el espacio donde dos objetos de masa muy grande permiten que un tercer objeto (de mucha menos masa) mantenga una posición fija con respecto a los otros dos objetos. Estos puntos se conocen hoy como “puntos de Lagrange” y son necesarios para colocar sondas y telescopios en el espacio a grandes distancias de la Tierra con fines de investigación.

Puntos de Lagrange (NASA)
La llegada de las computadoras y la posibilidad de sistemas informáticos cada vez más potentes han brindado nuevas oportunidades para abordar el problema de los n-cuerpos en los últimos años. En 2008, un equipo de investigación llevó a cabo simulación Lo que desató un debate entre expertos y entusiastas de la órbita: recopiló la mayor cantidad de información posible sobre nuestro sistema solar y trató de predecir qué pasaría con cada planeta que lo forma en los próximos 5 mil millones de años.
El grupo de investigación realizó más de dos mil simulaciones, partiendo siempre de las mismas condiciones excepto en un caso: la distancia entre el Sol y Mercurio, el planeta más cercano a nuestra estrella. En cada simulación se cambió la distancia unos milímetros para ver si esta diferencia podía tener consecuencias a muy largo plazo para el resto de planetas (entre el Sol y Mercurio hay una media de 58 millones de kilómetros). En el 1% de las simulaciones, la órbita de Mercurio cambió con el tiempo hasta el punto de que el planeta podría colisionar con el Sol o su vecino más cercano, Venus. En una simulación, un cambio inicial en la órbita de Mercurio fue suficiente para desestabilizar todo el sistema solar interior, que incluye, además de Mercurio y Venus, la Tierra, la Luna, Marte y sus dos lunas.
El artículo es un buen ejemplo de las dificultades que plantea el problema de los n-cuerpos. De hecho, el sistema en sí no es completamente aleatorio: si siempre comenzamos muchas simulaciones desde las mismas condiciones iniciales, siempre obtendremos el mismo resultado, pero si modificamos una variable aunque sea por un valor pequeño, a la larga el resultado cambia: es la definición de un sistema caótico. La cantidad de variables complica los cálculos hasta tal punto que es imposible llegar a una solución general del problema, que se aplique a todos los casos posibles.
Como hemos visto, el problema puede controlarse de alguna manera, pero todavía no es una cuestión trivial, y cuando se encuentran límites de este tipo, a menudo prevalecen consideraciones filosóficas. Pero nuevamente, como escribió Liu Cixin en su novela: “¿Debería la filosofía liderar los experimentos, o los experimentos deberían liderar la filosofía?”
Continuar publicando


